Recta perpendicular

Una Recta es una sucesión infinita de puntos, situados todos en una misma dirección, en tanto, esa sucesión se caracteriza por ser continua e indefinida, por tanto, una recta no tiene ni principio ni fin; junto al Plano y al Punto, la Recta es uno de los Entes geométricos fundamentales.

·         Una recta es una sucesión infinita de puntos, situados en una misma dirección.

o    Una recta tiene una sola dimensión: La longitud.

o    Las rectas se nombran mediante dos de sus puntos o por una letra minúscula.

o    Dos puntos determinan una recta.

 

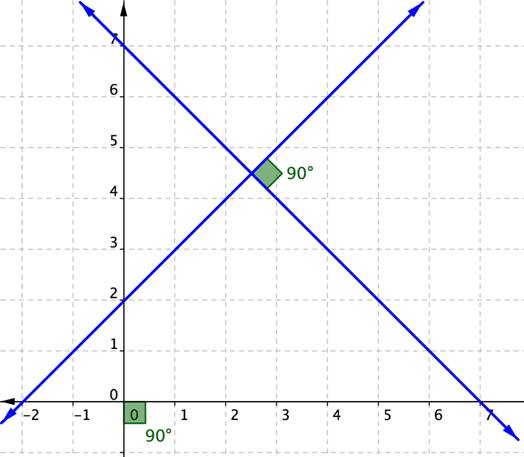
Rectas Perpendiculares. Dos rectas en el plano son perpendiculares si entre ellas forman un Ángulo recto (en rigor, se formen cuatro ángulos rectos). En un sistema de coordenadas, el producto de las pendientes de ambas rectas es -1.

·         Dos rectas son perpendiculares cuando al cortarse forman cuatro Ángulos iguales de 90º.

·         Dos rectas son perpendiculares si sus vectores directores son perpendiculares.

·         Dado un Punto perteneciente a una recta o exterior a ella, por él pasa una y sólo una perpendicular a dicha Recta.

Dos rectas son perpendiculares si sus Vectores directores son perpendiculares es decir el producto de los vectores es igual a cero

Si dos rectas son perpendiculares tienen sus pendientes inversas y cambiadas de signo.

La relación de perpendicularidad se puede dar entre:

·         Rectas: dos rectas coplanarias son perpendiculares cuando, al cortarse, dividen al plano en cuatro regiones iguales, cada una de los cuales es un ángulo recto. Al punto de intersección de dos rectas perpendiculares se le llama pie de cada una de ellas en la otra.

·         Semirrectas: dos semirrectas son perpendiculares, cuando conforman ángulos rectos teniendo o no el mismo punto de origen.

·         Planos: dos planos son perpendiculares cuando conforman cuatro ángulos diedros de 90º.

·         Semiplanos: dos semiplanos son perpendiculares cuando conforman ángulos diedros de 90°; generalmente, compartiendo la misma recta de origen.

Además, puede existir una relación de perpendicularidad entre los cuatro elementos anteriores, tomados de dos en dos.

Si dos rectas al cortarse forman Ángulos adyacentes congruentes, son perpendiculares. Por analogía, si dos planos al cortarse forman ángulos diedros adyacentes congruentes, son perpendiculares. Los lados de un ángulo diedro y sus semiplanos opuestos determinan dos planos perpendiculares).

DEFINICIÓN.- Un triángulo Rectángulo es un Triángulo uno de cuyos ángulos es recto. El lado opuesto al ángulo recto se llama hipotenusa y los otros dos lados son los catetos.

DEFINICIÓN.- Una recta y un plano son perpendiculares, si se intersecan y además, toda recta en el plano que pase por el punto de intersección es perpendicular a la recta dada.

Propiedades de las Rectas Perpendiculares

Las propiedades que ostentan las mismas son:

·         Reflexiva: La perpendicularidad no cumple con el carácter reflexivo.

·         Simétrica: Si una recta es perpendicular a otra, ésta es perpendicular a la primera.

·         Transitiva: La perpendicularidad no cumple con el carácter transitivo.

Teoremas

·         Teorema: En un plano, dos rectas perpendiculares a una tercera son paralelas.

·         Teorema: En un plano dado y por un punto dado de una recta dada, pasa una y solamente una recta perpendicular a la recta dada.

·         Teorema de la mediatriz: En un plano dado, la mediatriz de un segmento es la recta perpendicular al segmento en su punto medio.

·         Teorema: Desde un punto externo dado, hay a lo menos una recta perpendicular a la recta dada.

COLORARIO: Ningún Triángulo tiene dos Ángulos rectos.

·         Teorema - Si B y C equidistan de P y Q entonces todo punto entre B y C también equidistan de P y Q.

COROLARIO: Se da un segmento AB (con raya arriba) y la recta L en el mismo plano. Si dos puntos de L equidistan de A y B, entonces la mediatriz de AB (con raya arriba).

·         Teorema - Si una recta es perpendicular a dos rectas que se intersecan en su Punto de intersección, entonces es perpendicular al plano que contiene a las rectas.